Study Guide: Systems of Linear Equations
Solving systems of linear equations.
What are Systems of Linear Equations?
Solve more complex questions. Some questions are too complex to describe with one equation. When we need more equations, we create systems of equations.
Once we have accurately described a situation with multiple equations, we use algebraic methods such as Elimination to isolate the variables.
Variable in all equations must be related. In any system of equations, each set of facts is described with a unique equation. The trick is to be sure that each variable means the same thing in every equation of the system.
For example, if $c$ means “the number of cats” in one equation, it must mean “the number of cats” in every equation of that system.
How many solutions?
It helps to know that there are only three possible types of solutions for any system of linear equations. The can be seen by graphing (drawing) the lines of each equation.
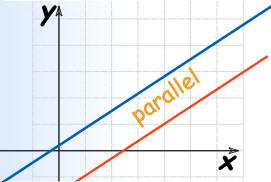
- No solution: The lines are parallel and never intersect (meet).
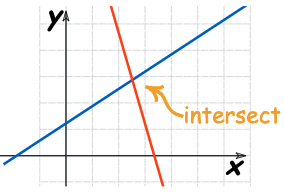
- One solution: The lines intersect (meet) at one point.
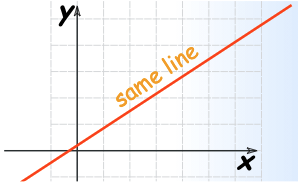
- Infinite solutions: The lines are parallel and have the same y-intercept, which mean the graphs of these lines are in identical positions.
Consistence and Dependence
Mathematicians always look for ways to say things in the easiest, shortest and most clearly accurate way. For this reason, they developed names for every possible combination of solutions. With these names, we can say, “This system is inconsistent.”, which is slightly easier than saying, “This system does not have any solutions.”
I know. It’s a small difference, but it adds up fast when we need to talk about many different systems at once, such as when researching the causes of cancer, modeling human-induced climate change, tracking a global pandemic, playing the stock market, or sending a rocket to Mars.
- Inconsistent: There are no solutions. The lines never intersect (meet).
- Consistent: There are one or more solutions. The lines intersect (meet) at one or more places.
- Independent: Each equation gives new information. They describe different and unique facts about the question.
- Dependent: The equations are mathematically identical, and will overlap on top of each other.
Consistency and Dependence
| Inconsistent |
Consistent |
| |
Independent |
Dependent |
 |
 |
 |
| No solution
| One solution
| Infinite solutions
|
Number-Digit Challenges
A: Value of First Digit is Greater
There is an unknown two digit number. The sum of its digits is 5. When these digits are reversed, the new number is 27 less than the original number. What is the original number?
- We are told that the sum of the digits is 5.
- Let $t$ be the digit in the tens column.
- Let $u$ be the digit in the units (ones) column.
- Write an equation for the sum of these digits (ignoring place value).
- We are told that the reversed number is 27 less than the original.
- Write an equation for the difference of the two numbers (including place value).
Place Value
Understanding place value is essential for solving this problem. In the above equation we intentionally ignored place value, as $t$ and $u$ stand for specific digits and we wanted to create an equation for the sum of the digits, NOT for the value of the two-digit number as a whole.
In this next step we create another equation, this time including place value. For example, when the digit symbolized by $t$ is in the tens place it's actual value in the whole number is ($10 \times t)$ or $10t$, and when it's in the one's place it's value in the whole number is ($1 \times t$) or simply $t$.
We will soon combine our two equations into a system of equations to solve the problem.
\begin{aligned}{}
(10 \times t) + (1 \times u) &= \textit{Value of original number} \\
(10 \times u) + (1 \times t) &= \textit{Value of reverse number} \\
-27 &= \textit{Difference}
\end{aligned}
Combine like terms, and get all variables on the left side.
Create a system of equations and add to eliminate one variable.
B: A Similar Example
There is an unknown two digit number. The sum of its digits is 13. When these digits are reversed, the new number is 9 less than the original number. What is the original number?
- We are told that the sum of the digits is 13.
- Let $t$ be the digit in the tens column.
- Let $u$ be the digit in the units (ones) column.
- Write an equation for the sum of these digits (ignoring place value).
- We are told that the reversed number is 9 less than the original.
- Write an equation for the difference of the two numbers (including place value).
Place Value
Understanding place value is essential for solving this problem. In the above equation we intentionally ignored place value, as $t$ and $u$ stand for specific digits and we wanted to create an equation for the sum of the digits, NOT for the value of the two-digit number as a whole.
In this next step we create another equation, this time including place value. For example, when the digit symbolized by $t$ is in the tens place it's actual value in the whole number is ($10 \times t)$ or $10t$, and when it's in the one's place it's value in the whole number is ($1 \times t$) or simply $t$.
We will soon combine our two equations into a system of equations to solve the problem.
\begin{aligned}{}
(10 \times t) + (1 \times u) &= \textit{Value of original number} \\
(10 \times u) + (1 \times t) &= \textit{Value of reverse number} \\
-9 &= \textit{Difference}
\end{aligned}
Combine like terms, and get all variables on the left side.
Create a system of equations and add to eliminate one variable.
C: Value of Second Digit is Greater
There is an unknown two digit number. The sum of its digits is 12. When these digits are reversed, the new number is 54 greater than the original number. What is the original number?
- We are told that the sum of the digits is 12.
- Let $t$ be the digit in the tens column.
- Let $u$ be the digit in the units (ones) column.
- Write an equation for the sum of these digits (ignoring place value).
- We are told that the reversed number is 54 greater than the original.
- Write an equation for the difference of the two numbers (including place value).
Place Value
Understanding place value is essential for solving this problem. In the above equation we intentionally ignored place value, as $t$ and $u$ stand for specific digits and we wanted to create an equation for the sum of the digits, NOT for the value of the two-digit number as a whole.
In this next step we create another equation, this time including place value. For example, when the digit symbolized by $t$ is in the tens place it's actual value in the whole number is ($10 \times t)$ or $10t$, and when it's in the one's place it's value in the whole number is ($1 \times t$) or simply $t$.
We will soon combine our two equations into a system of equations to solve the problem.
\begin{aligned}{}
(10 \times t) + (1 \times u) &= \textit{Value of original number} \\
(10 \times u) + (1 \times t) &= \textit{Value of reverse number} \\
54 &= \textit{Difference}
\end{aligned}
Combine like terms, and get all variables on the left side.
Create a system of equations and add to eliminate one variable.
D: Value of Both Digits is Equal
There is an unknown two digit number. The sum of its digits is 6. When these digits are reversed, the new number is the same as the original number. What is the original number?
- We are told that the sum of the digits is 6.
- Let $t$ be the digit in the tens column.
- Let $u$ be the digit in the units (ones) column.
- Write an equation for the sum of these digits (ignoring place value).
- We are told that the reversed number is the same as the original.
- Write an equation for the difference of the two numbers (including place value).
Place Value
Understanding place value is essential for solving this problem. In the above equation we intentionally ignored place value, as $t$ and $u$ stand for specific digits and we wanted to create an equation for the sum of the digits, NOT for the value of the two-digit number as a whole.
In this next step we create another equation, this time including place value. For example, when the digit symbolized by $t$ is in the tens place it's actual value in the whole number is ($10 \times t)$ or $10t$, and when it's in the one's place it's value in the whole number is ($1 \times t$) or simply $t$.
We will soon combine our two equations into a system of equations to solve the problem.
\begin{aligned}{}
(10 \times t) + (1 \times u) &= \textit{Value of original number} \\
(10 \times u) + (1 \times t) &= \textit{Value of reverse number} \\
0 &= \textit{Difference}
\end{aligned}
Combine like terms, and get all variables on the left side.
Create a system of equations and add to eliminate one variable.
E: Zero in Units Place
There is an unknown two digit number. The sum of its digits is 7. When these digits are reversed, the new number is 63 less than the original number. What is the original number?
- We are told that the sum of the digits is 7.
- Let $t$ be the digit in the tens column.
- Let $u$ be the digit in the units (ones) column.
- Write an equation for the sum of these digits (ignoring place value).
- We are told that the reversed number is 63 less than the original.
- Write an equation for the difference of the two numbers (including place value).
Place Value
Understanding place value is essential for solving this problem. In the above equation we intentionally ignored place value, as $t$ and $u$ stand for specific digits and we wanted to create an equation for the sum of the digits, NOT for the value of the two-digit number as a whole.
In this next step we create another equation, this time including place value. For example, when the digit symbolized by $t$ is in the tens place it's actual value in the whole number is ($10 \times t)$ or $10t$, and when it's in the one's place it's value in the whole number is ($1 \times t$) or simply $t$.
We will soon combine our two equations into a system of equations to solve the problem.
\begin{aligned}{}
(10 \times t) + (1 \times u) &= \textit{Value of original number} \\
(10 \times u) + (1 \times t) &= \textit{Value of reverse number} \\
-63 &= \textit{Difference}
\end{aligned}
Combine like terms, and get all variables on the left side.
Create a system of equations and add to eliminate one variable.
F: Quiz
There is an unknown two digit number. The sum of its digits is 11. When these digits are reversed, the new number is 27 less than the original number. What is the original number?
- We are told that the sum of the digits is 11.
- Let $t$ be the digit in the tens column.
- Let $u$ be the digit in the units (ones) column.
- Write an equation for the sum of these digits (ignoring place value).
- We are told that the reversed number is 27 less than the original.
- Write an equation for the difference of the two numbers (including place value).
Place Value
Understanding place value is essential for solving this problem. In the above equation we intentionally ignored place value, as $t$ and $u$ stand for specific digits and we wanted to create an equation for the sum of the digits, NOT for the value of the two-digit number as a whole.
In this next step we create another equation, this time including place value. For example, when the digit symbolized by $t$ is in the tens place it's actual value in the whole number is ($10 \times t)$ or $10t$, and when it's in the one's place it's value in the whole number is ($1 \times t$) or simply $t$.
We will soon combine our two equations into a system of equations to solve the problem.
\begin{aligned}{}
(10 \times t) + (1 \times u) &= \textit{Value of original number} \\
(10 \times u) + (1 \times t) &= \textit{Value of reverse number} \\
-27 &= \textit{Difference}
\end{aligned}
Combine like terms, and get all variables on the left side.
Create a system of equations and add to eliminate one variable.
G: Quiz 2
There is an unknown two digit number. The sum of its digits is 10. When these digits are reversed, the new number is 54 greater than the original number. What is the original number?
- We are told that the sum of the digits is 10.
- Let $t$ be the digit in the tens column.
- Let $u$ be the digit in the units (ones) column.
- Write an equation for the sum of these digits (ignoring place value).
- We are told that the reversed number is 54 greater than the original.
- Write an equation for the difference of the two numbers (including place value).
Place Value
Understanding place value is essential for solving this problem. In the above equation we intentionally ignored place value, as $t$ and $u$ stand for specific digits and we wanted to create an equation for the sum of the digits, NOT for the value of the two-digit number as a whole.
In this next step we create another equation, this time including place value. For example, when the digit symbolized by $t$ is in the tens place it's actual value in the whole number is ($10 \times t)$ or $10t$, and when it's in the one's place it's value in the whole number is ($1 \times t$) or simply $t$.
We will soon combine our two equations into a system of equations to solve the problem.
\begin{aligned}{}
(10 \times t) + (1 \times u) &= \textit{Value of original number} \\
(10 \times u) + (1 \times t) &= \textit{Value of reverse number} \\
54 &= \textit{Difference}
\end{aligned}
Combine like terms, and get all variables on the left side.
Create a system of equations and add to eliminate one variable.
H: Quiz 3
There is an unknown two digit number. The sum of its digits is 11. When these digits are reversed, the new number is 63 less than the original number. What is the original number?
- We are told that the sum of the digits is 11.
- Let $t$ be the digit in the tens column.
- Let $u$ be the digit in the units (ones) column.
- Write an equation for the sum of these digits (ignoring place value).
- We are told that the reversed number is 63 less than the original.
- Write an equation for the difference of the two numbers (including place value).
Place Value
Understanding place value is essential for solving this problem. In the above equation we intentionally ignored place value, as $t$ and $u$ stand for specific digits and we wanted to create an equation for the sum of the digits, NOT for the value of the two-digit number as a whole.
In this next step we create another equation, this time including place value. For example, when the digit symbolized by $t$ is in the tens place it's actual value in the whole number is ($10 \times t)$ or $10t$, and when it's in the one's place it's value in the whole number is ($1 \times t$) or simply $t$.
We will soon combine our two equations into a system of equations to solve the problem.
\begin{aligned}{}
(10 \times t) + (1 \times u) &= \textit{Value of original number} \\
(10 \times u) + (1 \times t) &= \textit{Value of reverse number} \\
-63 &= \textit{Difference}
\end{aligned}
Combine like terms, and get all variables on the left side.
Create a system of equations and add to eliminate one variable.
Test
$$ 26 \div 12.000000 = 2.166667 \text{ Remainder: } 2 $$
$$ 26 \div 12.000000 = $$
$$ 24 \div 12.000000 = 2.000000 \text{ Remainder: } 0 $$
$$ 24 \div 12.000000 = $$
$$ 144 \div 12.000000 = 12.000000 \text{ Remainder: } 0 $$
$$ 144 \div 12.000000 = $$
Source: https://class.ronliskey.com/study/mathematics-8/systems_of_equations/





