Study Guide: Slope
What is Slope?
The steepness of a mountain is called its slope. The same goes for the steepness of a mathematical line.
The slope of a mathematical line is one of its fundamental characteristics. We can use it to measure the rate of change.
The slope of a line is the ratio of the change on the y-axis to the change on x-axis. This is also called the rise over run.
Another way of saying this is: The slope is the rate of change of y with respect to x.
Notation
We write this ratio using two values:
- rise (or vertical change on the y-axis)
- run (or horizontal change along the x-axis)
Note: Mathematicians often say “delta” when talking about a rate of change. Delta can be written with the symbol $\Delta$.
$$Slope = \dfrac{rise}{run} = \dfrac{\textit{change in y}}{\textit{change in x}} = \dfrac{\Delta y}{\Delta x}$$
The Slope Formula
The slope of a line is usually represented by the letter $m$. We identify the location of each point by finding their x- and y-coordinates. The coordinates of first point are labeled as $(x_1, y_1)$, and the second point as $(x_2, y_2)$. Putting all this together we get the Slope Formula.
$$m = \dfrac{y_2−y_1}{x_2−x_1}$$
Careful! Subtraction is NOT Commutative
To find the slope, you subtract any point on the line from any other point on the line.
But! You MUST subtract the $\textit{ x-}$ and $\textit{ y-coordinates}$ in the same order in both the numerator and denominator!
If you set up the numerator as $y_2 – y_1$, you must use $x_2 – x_1$ in the denominator, not $x_1 – x_2$.
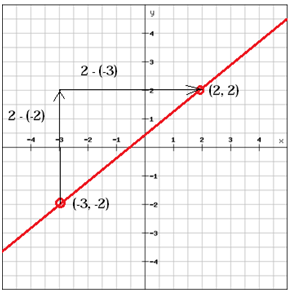
Example 1: Positive Slope
A line with a positive slope $(m > 0)$ rises as it goes from left to right.
$$ \begin{align} \textit{Let } P_1 &= \textit{the first point} \\\ P_2 &= \textit{the second point} \\[3ex] \hline P_1 &= (x_1, y_1) = (-3, -2) \\\ P_2 &= (x_2, y_2) = (2, 2) \end{align} $$
$$m=\left\{\dfrac{y_2 − y_1}{x_2 - x_1}\right\} = \left\{\dfrac{2 − (−2)}{2 − (−3)}\right\} = \left\{\dfrac{2 + 2}{2 + 3}\right\} = \dfrac{4}{5}$$
Example 2: Negative Slope
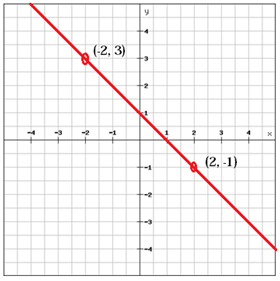
A line with a negative slope $(m < 0)$ falls as it goes from left to right.
$$m=\dfrac{y_2 – y_1}{x_2 - x_1} = \dfrac{-1 – 3}{2 – (-2)} = \dfrac{-1 – 3}{2 + 2} = \dfrac{–4}{4}=; –1$$
Parallel Lines
Lines with the same slope are parallel.
Slope-Intercept Form
$$ \begin{align} {\color{red}m} &=\textit{the slope} \\\ {\color{darkgreen}b}&=\textit{the y–intercept} \\[3ex] \hline y&={\color{red}m}x+{\color{darkgreen}b} \end{align} $$