Study Guide: Pythagorean Theorem
The Beautiful Theorem
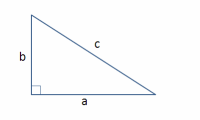
The square of the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides.
There are over 300 proofs for the Pythagorean Theorem, including one by a 12-year-old Albert Einstein, who then used the theorem two decades later to study Relativity Theory. Leonardo da Vinci and US President James A. Garfield also discovered original proofs.
The Theorem and Pythagoras (569 BCE – 475 BCE)
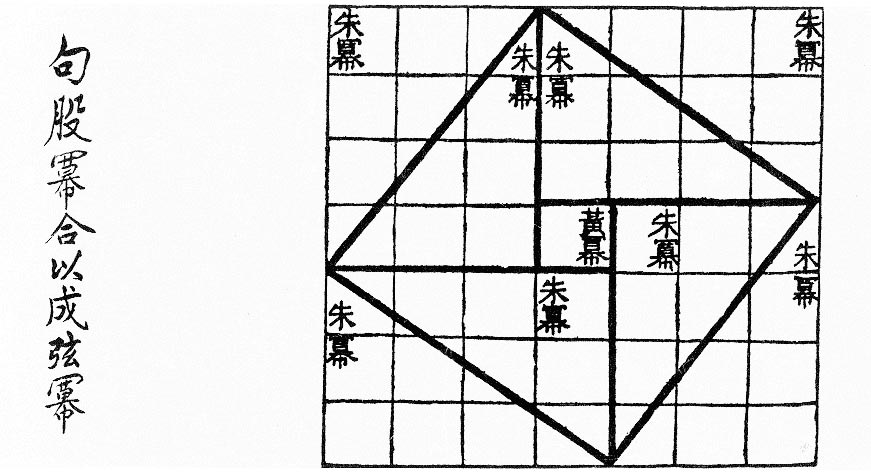
The theorem is named after Pythagoras of Samos (569 BCE – 475 BCE), however there is solid evidence that it was known to the Chinese over 1000 years before Pythagoras and is contained in one of the oldest Chinese mathematical texts, “Zhou Bi Suan Jing”. The Babylonians, Indians, and perhaps many other cultures also knew of it long before Pythagoras.
The name Pythagoras is now linked to the theorem because he believed it to represent an important principle of mathematics. He founded a famous school in what is now southern Italy. The school. called The Semicircle of Pythagoras, was both religious and scientific, and followed a strict code of secrecy.
Number Rules the Universe
Pythagoras taught that each number has divine meaning and studying the patterns of numbers could reveal the secrets of life. The was reflected in the Pythagorean motto, *“Number Rules the Universe”.
BTW: Pythagoras was an early feminist. Although social norms at the time forbade unmarried women from being in the company of men, his lectures were attended by both men and women, and some of his greatest students were women.

Right Triangles
Right triangles always have one 90 degree angle.
The two sides touching the right angle are the legs. The side opposite the right angle is called the hypotenuse.
The hypotenuse is always the longest side. In the Pythagorean Theorem, the legs are labeled $a$ and $b$, while the hypotenuse is labeled $c$.
Because addition is commutative, it does not matter which of the two legs is labeled $a$ or $b$, but there is always only one hypotenuse.
$$ a + b = b + a $$Area of Squares
The areas of the squares drawn next to a right triangle match the equation for the Pythagorean Theorem.
\begin{align} a^2 + b^2 &= c^2 \\\ 3^2 + 4^2 &= 5^2 \\\ 9 + 16 &= 25 \end{align}
Pythagorean Triplets
Pythagorean Triples are sets of three whole numbers that equal the side lengths of a Pythagorean Triangle. The set of Pythagorean Triples is infinite. The smallest Pythagorean Triple is (3, 4, and 5). We can generate more triples by scaling (multiplying) each value by the same amount.
Finding Triplets
| ${\color{white}n}$ | ${\color{white}(3n, 4n, 5n)}$ | Triplet |
|---|---|---|
| $n=2$ | $(3 \times 2), (4 \times 2), 5 \times 2)$ | ($6$, $8$, $10$) |
| $n=3$ | $(3 \times 3), (4 \times 3), 5 \times 3)$ | ($9$, $12$, $15$) |
| $n=4$ | $(3 \times (4, (4 \times 4), 5 \times 4)$ | ($12$, $16$, $20$) |
| Example Triplets | ||
|---|---|---|
| $(3, 4, 5)$ | $(5,12,13)$ | $(7, 24, 25)$ |
| $(8, 15, 17)$ | $(9, 40, 41)$ | $(11, 60, 61)$ |
| $(12,35, 37)$ | $(13, 84, 85)$ | $(15, 112, 113)$ |
| $(16, 63, 65)$ | $(17,144, 145)$ | $(19, 180, 181)$ |
| $(20, 21, 29)$ | $(20, 99, 101)$ | $(21, 220, 221)$ |
Sources
- https://en.wikipedia.org/wiki/Pythagorean_theorem
- https://link.springer.com/article/10.1057/jt.2009.16
- https://socratic.org/questions/what-was-the-original-proof-that-pythagoras-himself-used-to-prove-his-theorem-1



