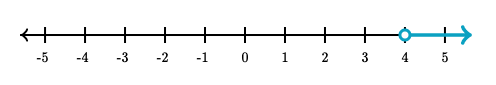Study Guides | inequalities | Inequalities Overview

Study Guide: Inequalities Overview

3 Introduction to Inequalities

Definition of Inequality: An algebraic relation showing that one quantity is greater than or less than another quantity.

Notation

The Law of Trichotomy: Every real number is either positive, negative, or zero.

Given any two real numbers, \( a \) and \( b \), exactly one of the following conditions must be true.

\[ a = b \] \[ a \gt b \] \[ a \lt b \]

Examples

    <tr>
        <td style="text-align:center">\( \gt \)</td>
        <td>Greater than</td>
        <td>\( x + 3 \gt 2 \)</td>
    </tr>

    <tr>
        <td style="text-align:center">\( \lt \)</td>
        <td>Less than</td>
        <td>\( x + 3 \lt 2 \)</td>
    </tr>

    <tr>
        <td style="text-align:center">\( \ge \)</td>
        <td>Greater than or equal to</td>
        <td>\( x + 3 \ge 2 \)</td>
    </tr>

    <tr>
        <td style="text-align:center">\( \le \)</td>
        <td>Less than or equal to</td>
        <td>\( x + 3 \le 2 \)</td>
    </tr>
    <tr>
    <th colspan="3">The following options go a little crazy with the negation.</th>
    </tr>
    <tr>
        <td style="text-align:center">\( \nless \)</td>
        <td>Not less than </td>
        <td>\( x + 3 \nless 2 \)</td>
    </tr>

    <tr>
        <td style="text-align:center">\( \ngtr \)</td>
        <td>Not greater than </td>
        <td>\( x + 3 \ngtr 2 \)</td>
    </tr>
    <tr>
        <td style="text-align:center">\( \nleq \)</td>
        <td>Not less than or equal to</td>
        <td>\( x + 3 \nleq 2 \)</td>
    </tr>

    <tr>
        <td style="text-align:center">\( \ngeq \)</td>
        <td>Not greater than or equal to</td>
        <td>\( x + 3 \ngeq 2 \)</td>
    </tr>
<tbody>

3-1. Graphing Inequalities

We can use a number line to show the possible solutions to an inequality.

Example 1: Greater Than

1. Draw an open circle to show that the number is not included in the solution.
2. Draw an arrow going toward the right.

\[ x \gt 4 \]

Example 2: Less Than or Equal

1. Draw a solid circle to show that the number is included in the solution.
2. Draw an arrow going toward the left.

\[ y \le 3 \]

Inequality Key Phrases

• “at least” means “greater than or equal to” or \( \ge \)
• “no more than” means “less than or equal to” or \( \le \)
• “no less than” means “more than or equal to” or \( \ge \)
• “more than” means “greater than” \( \gt \)
• “less than” means “less than” \( \lt \)

Many inequalities can be solved the same way we solve equations—by adding, subtracting, multiplying and dividing both sides of the inequality until the variable is isolated on one side.

Example 1: Simple Inequality

We can simplify this inequality without affecting the direction of the inequality symbol:

\begin{align} 3x &\lt 7+3 &&\text{Given: } 3x \text{ is less than } 7 + 3. \tag 1 \\[2ex] 3x &\lt 10 &&\text{Combine like terms.} \tag 2 \\[2ex] \dfrac{3x}{\color{red}{3}} &\lt \dfrac{10}{\color{red}{3}} &&\text{Divide both sides by 3.} \tag 3 \\[2ex] x &\lt \dfrac{10}{3} &&\text{Solution.} \tag 4 \\[2ex] \end{align}

3-2. Solving Inequalities

Example 2: Reversing the Inequality

We can swap sides of an inequality at any time as long as we also swap the inequality sign.

\begin{align} 12 &\lt x + 5 &&\text{Given.} \tag 1 \\[2ex] 12 {\color{red}- 5} &\lt x + 5 {\color{red}- 5} &&\text{Isolate the variable.} \tag 2 \\[2ex] 7 &\lt x &&\text{Simplified.} \tag 3 \\[2ex] x &\gt 7 &&\text{Solution: Sides reversed.} \tag 4 \end{align}

3-3. Dividing by a Negative Value

\begin{align} −2y &\lt −8 &&\text{Given.} \tag 1 \\[2ex] \dfrac{-2y}{\color{red}{-2}};&{\color{red}\gt};\dfrac{−8}{\color{red}{-2}} &&\text{Divide by }{\color{red}{-2}}\text{ and reverse the sign.} \tag 2 \\[2ex] y &\gt 4 &&\text{Solution.} \tag 3 \end{align}

Careful!

1. There are two operations that will reverse the direction of the inequality:
   1. Multiplying or dividing both sides by a negative number
   2. Reversing the left and right sides of the inequality
2. Don’t multiply or divide by a variable unless you know if it will always be either positive or always negative. If you know it will always be negative, you must also reverse the equality symbol.