Study Guides | number theory | Absolute Value

Study Guide: Absolute Value

Notation

The notation for the absolute value of $ p $ is $ \left| p \right| $.

Think of $ \left| p \right| $ as the distance of $ p $ from the origin on a number line.

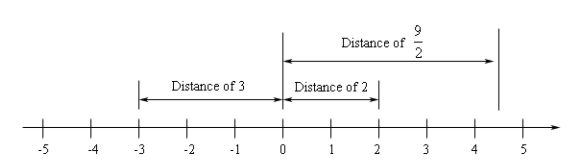
This shows that:

1. The distance from -3 to 0 is 3.
2. The distance from 2 to 0 is 2.
3. The distance from $ \frac{9}{2} $ to 0 is $ \frac{9}{2} $.
4. The distance from 0 to 0 is 0.

Thus:

$$ \left| 2 \right| = 2 \hspace{0.25in} \left| { - 3} \right| = 3 \hspace{0.25in} \left| {\frac{9}{2}} \right| = \frac{9}{2} \hspace{0.25in} \left| 0 \right| = 0 $$

Absolute Value Equations

Example 1: Isolating the absolute value expression

In most equations with variables, our goal is to isolate the variable. In absolute value equations, our goal is to isolate the absolute value expression.

\begin{align} 4 \left| x + 2 \right| &= 24 &&\text{Given.} \tag 1 \\[2ex] 4 \frac{\left| x + 2 \right|}{\color{red}{4}} &= \frac{24}{\color{red}{4}} &&\text{Isolate absolute value expression.} \tag 2 \\[2ex] \left| x + 2 \right| &= 6 &&\text{Simplified.} \tag 3 \\[4ex] x + 2 ; \color{red}{ - 2} &= -6 ; \color{red}{ - 2} &&\text{Case 1.} \tag 4 \\\\ x &= -8 \\[4ex] x + 2 ; \color{red}{ - 2} &= 6 ; \color{red}{ - 2} &&\text{Case 2.} \tag 5 \\\\ x &= 4 \\[4ex] x &= [-8, 4 ] &&\text{Solution set.} \tag 6 \end{align}

Example 2: Space Shuttle Valve

The diameter of a valve for the Space Shuttle must be within 0.001 mm of 5 mm. Installing a valve with a diameter outside of this range could cause the Space Shuttle to crash. Find the boundary values for an acceptable diameter of this valve.

Facts:

1. The ideal valve diameter is 5 mm.
2. The acceptable tolerance is \( \pm \) 0.001 mm.

Method:

1. Let x = the larger and smaller boundaries of the valve diameter.
2. Create an absolute value equation to define both boundaries at once.
3. Split the absolute-value equation into two cases:
   1. Case 1: Find the larger value by adding the acceptable tolerance to the ideal diameter.
   2. Case 2: Find the smaller boundary value by subtracting the acceptable tolerance from the ideal diameter.

\begin{align} \left| x - 5 \right| &= 0.001 &&\text{Equation} \tag 1 \\[2ex] x - 5 ; \color{red}{ + ; 5} &= - 0.001 ; \color{red}{ + ; 5} &&\text{Case 1} \tag 2 \\\\ x &= 4.999 &&\text{Smaller boundary value} \\[4ex] x - 5 ; \color{red}{ + ; 5} &= 0.001 ; \color{red}{ + ; 5} &&\text{Case 2} \tag 3 \\\\ x &= 5.001 &&\text{Larger boundary value} \\[4ex] x &= \{4.999, 5.001\} &&\text{Solution set} \tag 4 \end{align}