Study Guide: Area in the Coordinate Plane
Polygons in 2D Space
- Lines in the coordinate plane can form the sides of polygons.
- You can use points on these lines to find the area of the polygons.
Example
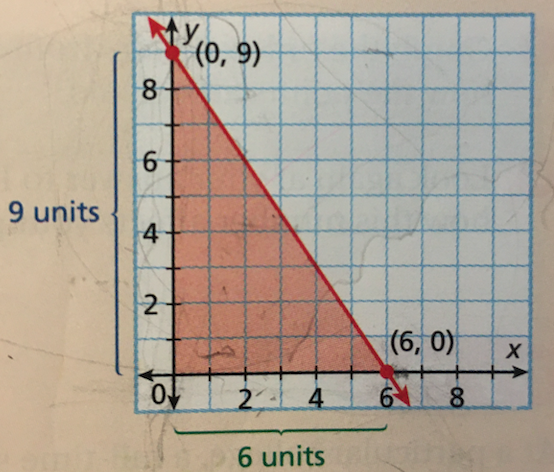
Find the area of the triangle formed by the x-axis, the y-axis, and the line given by the equation, $3x + 2y = 18$.
Step 1: Find the Intercepts
\begin{align} 3x + 2{\color{red}{y}} &= 18 &&\textit{Substitute 0 for y} \\\\ 3x + 2({\color{red}{0}}) &= 18 \\\\ 3x &= 18 \\\\ x &= 6 &&\textit{x-intercept} \end{align}
\begin{align} 3{\color{red}{x}} + 2y &= 18 &&\textit{Substitute 0 for x} \\\\ 3({\color{red}{0}}) + 2y &= 18 \\\\ y &= 9 &&\textit{y-intercept} \end{align}
Step 2: Graph the Line
- Use the intercepts to graph the line.
- The x-intercept is $6$, so mark the point at $(6, 0)$.
- The y-intercept is 9, so mark the point at $(0, 9)$.
- Draw a line going through both points.
Points in 2D Space
Step 3: Use the Right Triangle Area Formula
\begin{align} A &= \dfrac{1}{2}bh &&\textit{Formula} \\[3ex] &= \dfrac{1}{2}(6)(9) &&\textit{Substitute the base and height} \\[3ex] A &= 27 \text{ units}^2 &&\textit{Area of the triangle} \\[3ex] \end{align}
Graph
Exercises
1. Find the area of the triangle formed by the x-axis, the y-axis, and the line given by the equation, $3x + 2y = 12$.
2. Find the area of the triangle formed by the x-axis, the y-axis, and the line given by the equation, $y=6-x$.
3. What kind of polygon is formed by the x-axis, the y-axis, the line given by $y=6$, and the line given by $x=4$? What is its area?


